
Khoa Khoa học cơ bản thực hiện chuyên đề bồi dưỡng giảng viên năm học 2019-2020 với chủ đề “Phương trình vi phân và ứng dụng thực tiễn”
21:49 30/12/2019
Để nâng cao trình độ chuyên môn cho đội ngũ giảng viên trong khoa, tăng cường tính liên hệ ứng dụng thực tiễn của toán học. Từ ngày 26 đến 31/12/2019, khoa KHCB đã tổ chức bồi dưỡng giảng viên chuyên đề "Phương trình vi phân và ứng dụng thực tiễn" do TS. Nguyễn Viết Tuân giảng dạy.

ỨNG DỤNG CỦA PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG VÀO BÀI TOÁN Ô NHIỄM MÔI TRƯỜNG
05:58 28/11/2019
Ô nhiễm môi trường là vấn đề rất quan trọng mang tính chất toàn cầu. Đặc biệt là ô nhiễm không khí. Chúng ta có thể sử dụng ứng dụng của phương trình đạo hàm riêng để giải quyết các mô hình bài toán ô nhiễm không khí và nguồn nước. Tìm hiểu ứng dụng của phương trình đạo hàm riêng trong giải bài toán ô nhiễm không khí

ỨNG DỤNG PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG CẤP MỘT TRONG BÀI TOÁN MẠCH ĐIỆN
21:28 05/11/2019
Người ta thấy rằng hầu hết các quy luật của khoa học tự nhiên, của kinh tế, hay của kỹ thuật đều được phát biểu dưới dạng các phương trình đạo hàm riêng. Đặc biệt những kiến thức về phương trình đạo hàm riêng đã được ứng dụng vào ngành kỹ thuật điện.

Nghiệm thu đề tài cấp trường- bộ môn Toán
15:29 19/06/2019
Tháng 5 năm 2019 khoa Khoa học cơ bản tổ chức nghiệm thu đề tài khoa học cấp cơ sở năm học 2018-2019. Nhóm tác giả do đồng chí Nguyễn Thị Huệ (chủ nhiệm) triển khai thực hiện đề tài: “NGHIÊN CỨU TÍNH ỔN ĐỊNH NGHIỆM CỦA PHƯƠNG TRÌNH VI PHÂN VÀ ỨNG DỤNG KHẢO SÁT SỰ ỔN ĐỊNH CỦA HỆ THỐNG KỸ THUẬT, HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG”.

Khoa Khoa học Cơ bản tổ chức nghiệm thu đề tài cấp cơ sở
15:27 06/05/2019
Ngày 22 tháng 4 năm 2019, khoa Khoa học Cơ bản đã tiến hành nghiệm thu đề tài khoa học cấp khoa với hai đề tài 05.KHCN/18-19 “Nghiên cứu chế tạo vật liệu nanosilica ứng dụng chế tạo màng đổi màu” và 06.KHCN/18-19 “Nghiên cứu tính ổn định nghiệm của phương trình vi phân và ứng dụng khảo sát sự ổn định của hệ thống điều khiển tự động”.
Sự ổn định mũ của hệ phương trình vi phân phi tuyến theo phương pháp hàm Lyapunov
09:40 22/04/2019
Trong bài báo này, chúng tôi sử dụng phương pháp hàm Lyapunov đưa ra điều kiện đủ để hệ phương trình vi phân phi tuyến ổn định mũ bằng cách xác định tựa hàm Lyapunov. Ngoài ra, trong trường hợp phương trình vi phân phi tuyến có điểm cân bằng ổn định, thì chỉ ra được công thức xác định hàm Lyapunov trong lân cận compact của điểm cân bằng.

Sự ổn định nghiệm của hệ phương trình vi phân tuyến tính
19:31 27/11/2018
Từ những năm 60 của thế kỷ 20, do nhu cầu nghiên cứu các tính chất định tính các mô hình điều khiển kỹ thuật, người ta bắt đầu nghiên cứu tính ổn định các hệ điều khiển như bài toán điều khiển được, bài toán ổn định hoá, điều khiển tối ưu, vv…. Các bài toán kỹ thuật này thường được mô tả bởi các hệ phương trình vi phân. Do đó, sự ổn định nghiệm của hệ phương trình vi phân sẽ quyết định tính ổn định của hệ thống điều khiển.
Trong bài viết này, chúng tôi đề cập đến một số phương pháp xét sự ổn định của hệ phương trình vi phân tuyến tính.
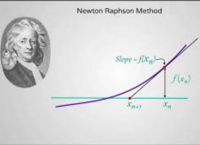
Phương pháp Newton Raphson giải phương trình phi tuyến
08:46 02/11/2018
Trong bài viết này tôi trình bày phương pháp Newton-Raphson để giải phương trình hoặc hệ phương trình phi tuyến.

Bộ môn Toán bảo vệ đề tài cấp cơ sở
07:32 01/06/2018
Ngày 31/5/2018, tại phòng họp trường Đại học Sao Đỏ, bộ môn Toán đã tiến hành bảo vệ đề tài khoa học cấp cơ sở: Phương trình vi phân ngẫu nhiên và ứng dụng vào một số bài toán kĩ thuật.
Phương trình vi - tích phân trung tính kiểu sóng khuếch tán
10:33 25/05/2018
Trong bài báo này, chúng tôi nghiên cứu sự tồn tại của nghiệm phân rã cho phương trình vi - tích phân trung tính kiểu sóng khuếch tán bằng cách sử dụng phương pháp điểm bất động.

Toán tử giải thức bậc phân số
21:21 10/05/2018
Phương trình vi phân hay phương trình sai phân là một phương trình toán học nhằm biểu diễn mối quan hệ giữa một hàm chưa được biết (một hoặc nhiều biến) với đạo hàm của nó (có bậc khác nhau). Phương trình sai phân đóng vai trò cực kì quan trọng trong kĩ thuật, vật lý, kinh tế và một số ngành khác. Do đó xác định nghiệm ổn định của phương trình vi phân có ý nghĩa thực tiễn rất thiết thực.
Chéo hóa, tam giác hóa ma trận và ứng dụng
16:29 23/03/2018
Những kiến thức đầu tên về ma trận đã xuất hiện từ những năm 152 TCN, trong cuốn sách “Cửu chương toán thuật” để giải hệ năm phương trình tuyến tính. Thuật ngữ trong tiếng Anh "matrix" (tiếng Latin là "womb", dẫn xuất từ mater—mẹ) do James JosephSylvester nêu ra vào năm 1850.

Giải phương trình tích phân Fedholm loại 2 bằng phương pháp thác triển theo tham số
15:31 18/01/2018
Phương pháp thác triển theo tham số giải phương trình toán tử được nghiên cứu trong các công trình của Trenoghin V.A., Fonarov A.A. và Gaponenco Iu. L. Trong bài viết này tôi nghiên cứu ứng dụng của phương pháp nói trên qua việc giải gần đúng phương trình toán tử, với toán tử tích phân Fredholm.
- Trường Đại học Sao Đỏ tổ chức “Tết sum vầy – Xuân ơn...
- Trường Đại học Sao Đỏ tổ chức hội nghị Giảng viên chủ...
- Khoa Khoa học cơ bản Hội thảo khoa học bộ môn với chủ...
- Khoa Khoa học cơ bản bồi dưỡng giảng viên với chuyên...
- Khoa Khoa học cơ bản Hội thảo khoa học bộ môn với chủ...
- VIET (Franciscus Viet)
-
Nghị định 73/2015/NĐ-CP
(Quy định về tiêu chuẩn phân tầng; khung xếp hạng và tiêu chuẩn xếp...) -
Quyết định số 07/QĐ-TTg của Thủ tướng...
(Về điều chỉnh mức cho vay đối với học sinh, sinh viên) -
Thông tư số 18/2015/TT-BKHCN
(Quy định thi đua, khen thưởng trong lĩnh vực khoa học và công nghệ) -
Thông tư số 43/2015/TT-BLĐTBXH
(Quy định về đào tạo thường xuyên) -
Nghị định số 137/2015/NĐ-CP
(Quy định chi tiết một số điều và biện pháp thi hành Luật Căn cước công...)











