Đẳng thức pohozaev và một vài ứng dụng

Đẳng thức pohozaev và một vài ứng dụng

 14:12 27/12/2017

. Bằng việc thiết lập các đẳng thức Pohozaev tương ứng cho phương trình, hệ phương trình và dựa vào cấu trúc hình học của miền đang xét, chúng tôi chứng tỏ được sự không tồn tại nghiệm của bài toán trên với một vài điều kiện cho trước.

Seminar bộ môn Toán: Một số phương pháp giải phương trình phi tuyến

Seminar bộ môn Toán: Một số phương pháp giải phương trình phi tuyến

 09:39 19/12/2017

Trong toán học, một hệ phương trình phi tuyến là một tập hợp các phương trình đồng thời trong đó các ẩn số (hoặc các hàm chưa biết trong trường hợp của phương trình vi phân) xuất hiện như các biến của một đa thức bậc cao hơn một hoặc trong các đối số của một hàm không phải là một đa thức bậc một. Để tìm hiểu phương pháp giải đơn giản nhất cho hệ phương trình phi tuyến, ngày 19 tháng 12 năm 2017, bộ môn Toán đã tổ chức seminar với chủ đề “Một số phương pháp giải phương trình phi tuyến”

Một số phương pháp giải phương trình phi tuyến

Một số phương pháp giải phương trình phi tuyến

 14:56 12/12/2017

Để tìm nghiệm đúng của phương trình phi tuyến là một vấn đề khá khó khăn khi giải toán. Có nhiều bài ta chỉ tìm được nghiệm gần đúng. Đối với phương trình phi tuyến ta có thể sử dụng một số phương pháp giải như: phương pháp lặp đơn, phương pháp dây cung, phương pháp Newton, Raphson…Ta cũng có thể sử dụng phần mềm Maple để giải.

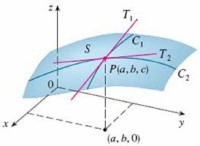
Sử dụng phương pháp số để giải gần đúng phương trình đạo hàm riêng

Sử dụng phương pháp số để giải gần đúng phương trình đạo hàm riêng

 00:09 11/11/2017

Phương trình đạo hàm riêng thường xuyên xuất hiện trong các bài toán ứng dụng của lý thuyết thuỷ động học, cơ học lượng tử, điện học, điện - từ trường,… Đa số các bài toán này rất phức tạp, nhiều bài toán không có nghiệm theo nghĩa cổ điển. Vấn đề tìm nghiệm đúng của các phương trình đạo hàm riêng không thể và cũng không cần thực hiện trong mọi trường hợp. Bởi vậy, ta dẫn đến việc chỉ tìm được nghiệm gần đúng của các phương trình đạo hàm riêng và cũng từ đó xuất hiện các phương pháp để giải gần đúng các phương trình đó.

Tin mới nhất
Văn bản pháp luật
 
Bạn đã không sử dụng Site, Bấm vào đây để duy trì trạng thái đăng nhập. Thời gian chờ: 60 giây