Đào tạo - Trang 3


Học vụ sinh viên	Học tập trực tuyến	Thư viện điện tử	Ký túc xá

Một số phương pháp không cổ điển giải bài toán giá trị ban đầu

09/01/2019 02:11:00 AM
Đã xem: 1375

Nhiều bài toán Cauchy tổng quát chưa có cách giải đúng, hoặc là cách giải đúng rất phức tạp. Khi đó, ta tìm cách giải gần đúng hoặc tìm các cách giải gián tiếp.

Chuẩn bị tốt cho những kỳ thi

27/12/2018 03:14:00 AM
Đã xem: 1516

Thời sinh viên của tôi (cách đây đã 10 năm rồi) luôn có câu truyền miệng rằng: “Bốn năm là tám kỳ thi - Học xong đại học còn gì là xuân”. Điều đó chứng tỏ rằng có áp lực không nhỏ đối với sinh viên qua những kỳ thi. Bây giờ, với tư cách là một giảng viên, tôi cho rằng để đạt được kết quả tốt trong các kỳ thi, sinh viên phải có sự chuẩn bị tốt một số yếu tố sau:

Kích thích hứng thú học tập các học phần Khoa học Cơ bản

13/12/2018 03:49:00 AM
Đã xem: 1282

Rời khỏi ghế phổ thông, sinh viên bắt đầu làm quen với giảng đường đại học từ những bài giảng của các môn khoa học cơ bản. Do đó, vai trò tạo động lực, định hướng cho sinh viên học tập và tu dưỡng rèn luyện đạo đức lối sống ngay từ những bước chân trên giảng đường đầu tiên là rất quan trọng.

Kĩ năng làm việc nhóm hiệu quả

27/11/2018 03:14:00 AM
Đã xem: 1563

Cho dù, bạn chưa hẳn ở vị trí lãnh đạo cao nhất nhưng hiểu rõ và biết cách xây dựng và thiết lập tinh thần làm việc chung sẽ giúp tạo thêm động lực làm việc cho nhân viên và mang lại nhiều lợi ích hơn cho cơ quan, công ty nơi bạn làm việc. Kết quả được xem là thành công khi đội nhóm bạn xây dựng làm việc hiệu quả và hoàn thành xuất sắc mọi công việc mục tiêu đề ra

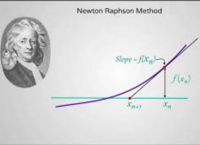
Phương pháp Newton Raphson giải phương trình phi tuyến

01/11/2018 09:46:00 PM
Đã xem: 5320

Trong bài viết này tôi trình bày phương pháp Newton-Raphson để giải phương trình hoặc hệ phương trình phi tuyến.

Hiện tượng Gibbs trong truyền tín hiệu

25/10/2018 06:34:00 AM
Đã xem: 1701

Hiện tượng Gibbs phản ánh những khó khăn vốn có trong việc xấp xỉ một hàm gián đoạn bởi một chuỗi hữu hạn các sóng sin và cosin liên tục. Điều quan trọng là nhấn mạnh vào từ hữu hạn bởi vì mặc dù mỗi một phần của chuỗi Fourier vượt quá chức năng mà nó xấp xỉ, giới hạn của các hàm thành phần thì không. Giá trị của x đạt cực đại đạt được gần và gần hơn với sự gián đoạn khi số lượng các điều kiện tổng hợp tăng lên, một khi vượt qua bởi một x đặc biệt, có thể hội tụ ở giá trị x.

Những ứng dụng của năng lượng mặt trời

06/09/2018 10:23:00 PM
Đã xem: 1391

Năng lượng mặt trời, bức xạ ánh sáng và nhiệt từ mặt trời đã được con người khai thác ngay từ thời cổ đại. Bức xạ mặt trời, cùng với tài nguyên thứ cấp của năng lượng mặt trời như sức gió và sức sóng, sức nước và sinh khối làm thành hầu hết năng lượng tái tạo có sẵn trên trái đất. Chỉ một phần rất nhỏ của năng lượng mặt trời có sẵn được sử dụng.

Mô hình chuỗi thời gian và thống kê Bayes

30/08/2018 09:25:00 PM
Đã xem: 1462

Trong phần này, chúng ta xem xét các mô hình tuyến tính chuỗi thời gian phổ biến nhất, cùng với phân tích Bayes và các liên kết Markov của chúng (mà có thể khai thác trong việc triển khai MCMC).

Bí ẩn dẫy số Fibonacci và sự trùng hợp kinh ngạc trong tự nhiên

07/06/2018 04:14:00 AM
Đã xem: 1377

Bạn đã bao giờ thực sự dành thời gian ngồi đếm số cánh của các loài hoa? Có lẽ là chưa. Nhưng nếu có thời gian, bạn sẽ nhận thấy một điều khá thú vị rằng: “ số lượng cánh hoa trên một bông hoa luôn là một trong các số thuộc dãy số Fibonacci”.

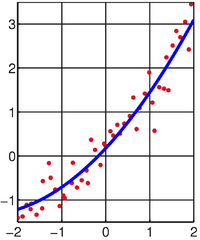
Phương pháp bình phương bé nhất và ứng dụng

03/05/2018 03:41:00 AM
Đã xem: 5569

Trong toán học cũng như trong nhiều bài toán thực tế, ta thường gặp bài toán liên quan đến khảo sát các tính chất của hàm số hoặc tính giá trị của hàm số tại một giá trị cụ thể. Tuy nhiên, hàm số đang xét không phải lúc nào cũng được cho dưới dạng biểu thức giả tích mà có thể chỉ cho dưới dạng bảng thể hiện mối liên hệ giữa giá trị hàm số và giá trị đối số tại một số hữu hạn điểm.

Những chú ý khi thi trắc nghiệm môn toán trong kỳ thi THPT Quốc gia năm 2018

02/05/2018 03:46:00 AM
Đã xem: 1392

Các em học sinh khối 12 sắp bước vào một trong những kỳ thi quan trọng nhất của đời học sinh. Cùng với quá trình ôn thi vừa qua, việc tận dụng tốt thời gian còn lại và có chiến lược thi cử hợp lý sẽ giúp các em có kết quả cao nhất với khả năng của mình. Dưới đây là những chia sẻ kinh nghiệm, lưu ý của thầy cô dành cho các sĩ tử trước kỳ thi THPT quốc gia 2018

Quang học và ứng dụng

26/04/2018 09:51:00 PM
Đã xem: 4241

Ánh sáng lung linh với lưỡng tính sóng hạt đã là nguồn cảm hứng cho nhiều khám phá vật lý quan trọng. Từ việc nghiên cứu tính chất của ánh sáng người ta đã phát hiện lưỡng tĩnh sóng hạt không chỉ đối với ánh sáng mà còn xảy ra với vật chất nói chung. Cũng chính từ việc nghiên cứu vận tốc ánh sáng mà Einstein đã phát minh ra thuyết tương đối hẹp và tương đối rộng. Trong báo cáo này, chúng tôi sẽ trình bày cơ sở lý thuyết cũng như một số ứng dụng hấp dẫn của quang học trong cuộc sống, trong kỹ thuật cũng như trong nghiên cứu khoa học.

Các yếu tố ảnh hưởng đến kỹ năng tự học của sinh viên

12/04/2018 10:36:00 PM
Đã xem: 9114

Để đánh giá thực trạng về nhu cầu, động cơ, hứng thú tự học của sinh viên, tác giả đã tiến hành cuộc điều tra sử dụng các câu hỏi mở thông qua phiếu điều tra. Đối tượng điều tra: Sinh viên ngành May năm thứ 2 (DK7-M)Trường Đại học Sao Đỏ.

Một số ứng dụng của số phức

06/04/2018 10:00:00 PM
Đã xem: 4839

Toán học nói chung và số phức nói riêng có nhiều ứng dụng trong khoa học, kỹ thuật và trong thực tế. Bài viết này xin trình bày một số ứng dụng hay của số phức khi giải các bài toán đại số, hình học, vật lý.

Dùng phương pháp lặp đơn giải hệ phương trình tuyến tính

04/04/2018 03:08:00 AM
Đã xem: 11117

Không phải hệ PTTT nào cũng tồn tại nghiệm đúng và có những hệ PTTT tồn tại ngiệm đúng nhưng quá trình tính toán dễ gặp sai số. Do đó, việc tìm được nghiệm gần đúng của hệ PTTT cuãng là điều rất hữu ích. Trong bài viết này tôi sẽ trình bày phương pháp lặp đơn để giải hệ PTTT, điều kiện của hệ để có thể áp dụng phương pháp lặp đơn, cách giải theo phương pháp lặp đơn bằng máy tính Casio.