Khoa Khoa học cơ bản - trường ĐH Sao Đỏ

Lịch các sự kiện thiên văn tháng 10 năm 2023

 15:35 08/10/2023

CHỮ SỐ VÀ NGUỒN GỐC

 10:42 01/10/2020

Có một điều ít ai biết, văn bản đầu tiên của nhân loại không phải thơ ca, văn chương hay luật pháp mà là toán học. Đó là tấm đất sét có niên đại 3.400-3.000 TCN, được tìm thấy trong khu vực văn minh Lưỡng Hà với nội dung: “29.086 (đơn vị) lúa mạch, 37 tháng”. Với các con số được ghi lại, chúng ta biết đó là văn bản (kế toán) mà ở đó các con số đã thực sự xuất hiện và giải quyết những nhu cầu tối quan trọng của xã hội loài người.

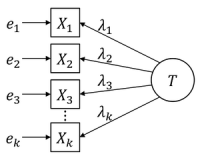
PHƯƠNG PHÁP PHÂN TÍCH ĐỘ TIN CẬY CRONBACH ALPHA VÀ PHÂN TÍCH NHÂN TỐ EFA TRONG CÁC PHÂN TÍCH ĐỊNH LƯỢNG

 07:20 29/08/2019

Phân tích EFA là một bước rất quan trọng khi thực hiện phân tích dữ liệu định lượng bằng SPSS trong một bài nghiên cứu khoa học. Khi kiểm định một lý thuyết khoa học, chúng ta cần đánh giá độ tin cậy của thang đo (phân tích Cronbach Alpha) và giá trị của thang đo (EFA).

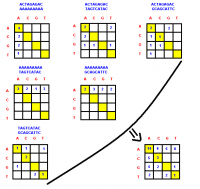
Chéo hóa, tam giác hóa ma trận và ứng dụng

 16:29 23/03/2018

Những kiến thức đầu tên về ma trận đã xuất hiện từ những năm 152 TCN, trong cuốn sách “Cửu chương toán thuật” để giải hệ năm phương trình tuyến tính. Thuật ngữ trong tiếng Anh "matrix" (tiếng Latin là "womb", dẫn xuất từ mater—mẹ) do James JosephSylvester nêu ra vào năm 1850.

Seminar bộ môn Toán: Một số phương pháp giải phương trình phi tuyến

 09:39 19/12/2017

Trong toán học, một hệ phương trình phi tuyến là một tập hợp các phương trình đồng thời trong đó các ẩn số (hoặc các hàm chưa biết trong trường hợp của phương trình vi phân) xuất hiện như các biến của một đa thức bậc cao hơn một hoặc trong các đối số của một hàm không phải là một đa thức bậc một. Để tìm hiểu phương pháp giải đơn giản nhất cho hệ phương trình phi tuyến, ngày 19 tháng 12 năm 2017, bộ môn Toán đã tổ chức seminar với chủ đề “Một số phương pháp giải phương trình phi tuyến”

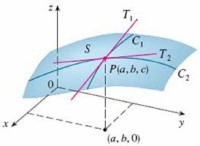
Sử dụng phương pháp số để giải gần đúng phương trình đạo hàm riêng

 00:09 11/11/2017

Phương trình đạo hàm riêng thường xuyên xuất hiện trong các bài toán ứng dụng của lý thuyết thuỷ động học, cơ học lượng tử, điện học, điện - từ trường,… Đa số các bài toán này rất phức tạp, nhiều bài toán không có nghiệm theo nghĩa cổ điển. Vấn đề tìm nghiệm đúng của các phương trình đạo hàm riêng không thể và cũng không cần thực hiện trong mọi trường hợp. Bởi vậy, ta dẫn đến việc chỉ tìm được nghiệm gần đúng của các phương trình đạo hàm riêng và cũng từ đó xuất hiện các phương pháp để giải gần đúng các phương trình đó.