
Nghiên cứu đặc tính đất sét Trúc Thôn và đánh giá khả năng ứng dụng của vật liệu trong mĩ phẩm
22:09 01/12/2021
Bài báo này sử dụng phương pháp phân tán và li tâm để phân riêng đất sét Trúc Thôn theo kích thước hạt. Các hạt đất sét thu được có kích thước trong khoảng 220nm – 530nm. Bằng các phương pháp phân tích hiện đại như phổ nhiễu xạ tia X (XRD), phổ huỳnh quang tia X (XRF), phổ khối lượng cao tần cảm ứng plasma ICP trên thiết bị ICP- OES đã xác định được thành phần khoáng chất gồm các khoáng mica muscovite, quazt, kaolinite, CaCO3, kyanite; thành phần hóa học chủ yếu là Al2O3, SiO2, K2O... Kết quả nghiên cứu cũng cho thấy, vật liệu đất sét đỏ Trúc Thôn còn chứa kim loại nặng với hàm lượng PbO là 130ppm, V2O5 là 324ppm; đất sét trắng có hàm lượng Pb là 80.130 ppm, hàm lượng As là 2.159ppm, Hg là 0.074ppm. Thay đổi pH của dung dịch đất sét bằng dung dịch HCl, đã tách được một lượng chì đáng kể (giảm 78%) trong mẫu, hàm lượng Pb còn lại 18.333 ppm.

SỬ DỤNG Saccharomyces cerevisiae RV002 ĐỂ LÊN MEN RƯỢU VANG TỪ QUẢ SIM (Rhodomyrtus tomentosa)
20:57 05/11/2021
Nghiên cứu được thực hiện nhằm đánh giá hiệu quả của chủng Saccharomyces cerevisiae RV002 khi lên men nguyên liệu sim được trồng và thu hoạch tại Chí Linh, Hải Dương. Các yếu tố như tỷ lệ nguyên liệu/nước (1,0/1,0 ÷ 1,0/2,0 w/v), tỷ lệ nấm men (0,15 ÷ 0,55 g/L), hàm lượng chất khô hòa tan (20 ÷ 24 oBx), pH ban đầu (3,5 ÷ 5,0), thời gian lên men (9,0 ÷ 13,0 ngày) đã được đánh giá mức độ ảnh hưởng và điều kiện phù hợp cho quá trình lên men. Nghiên cứu sử dụng phương pháp thiết kế thí nghiệm đơn yếu tố, kết hợp với phần mềm SPSS 22.0, Excel 2016 để xử lý số liệu thống kê. Kết quả cho thấy sau 11,0 ngày lên men ở tỷ lệ nguyên liệu/nước là 1,0/1,5 w/v, tỷ lệ nấm men là 0,45 g/L, hàm lượng chất khô hòa tan là 23 oBx, pH ban đầu là 4,0, nhiệt độ lên men là 28 ± 2oC nấm men hoạt độ hiệu quả và cho chất lượng rượu vang sim đạt mức chất lượng cảm quan tốt (theo TCVN 3215-79). Hàm lượng ethanol đạt 12,8±0,25 (% Vol.), hàm lượng đường sót là 0,28±0,02 (g/L), hàm lượng methanol là 330±1,5 (mg/L cồn 100o), hàm lượng SO2 là 263,45±1,7 (mg/L cồn 100o), hàm lượng ester là 0,23±0,03 (g/L). Chất lượng cảm quan và hóa học phù hợp với TCVN 7045-2013 và QCVN 6-3:2010/BYT.

TRƯỜNG ĐẠI HỌC SAO ĐỎ KẾT HỢP VỚI PHÒNG Y TẾ THÀNH PHỐ CHÍ LINH TỔ TỨC TIÊM PHÒNG VACXIN COVID CHO CÁN BỘ, GIẢNG VIÊN, SINH VIÊN
05:42 19/09/2021
Hiện nay tình hình dịch bệnh Covid 19 vẫn rất phức tạp. Với phương châm “5K + Vaccine + Công nghệ”, tập thể giảng viên, công nhân viên và sinh viên trường Đại học Sao Đỏ rất tích cực thực hiện các biện pháp 5K trong phòng chống dịch, đồng thời cũng ý thức được rằng việc tiêm Vacxin phòng Covid 19 là phương pháp hiệu quả nhất để phòng chống Covid, cũng là thể hiện được trách nhiệm với bản thân và cộng đồng.
TRƯỜNG ĐẠI HỌC SAO ĐỎ - NƠI THẮP SÁNG ƯỚC MƠ
21:40 18/08/2021
Trường Đại học Sao Đỏ là một trong những trường đi đầu trong công tác phòng, chống dịch bệnh cũng như hoàn thành tốt công tác giảng dạy. Trường đã nghiên cứu và áp dụng nhiều phương pháp giúp sinh viên được học tập trong môi trường an toàn nhất có thể.

Mô hình hồi quy đa biến phân tích các nhân tố ảnh hưởng đến quyết định chọn trường đại học Sao Đỏ của sinh viên
21:27 18/08/2021
Phân tích hồi quy là một phương pháp thống kê mà giá trị kỳ vọng của một hay nhiều biến được dự đoán dựa vào điều kiện của các biến ngẫu nhiên khác. Trong báo cáo này tác giả có sử dụng mô hình hồi quy đa biến để tìm hiểu mức độ ảnh hưởng của các nhân tố đến quyết định chọn trường Đại học Sao Đỏ của sinh viên. Kết quả nghiên cứu cho thấy những nhân tố có ảnh hưởng lớn nhất đến quyết định chọn trường là yếu tố danh tiếng, chi phí và chuẩn chủ quan.
Nguồn gốc của cách đếm
14:00 03/08/2021
Những thay đổi về số và lượng trong cuộc sống khiến cho con người nguyên thuỷ dần dần sản sinh ý thức về sự đếm. Họ muốn hiểu được sự khác biệt giữa "có" và "không", giữa "nhiều và "ít" và sự khác biệt giữa "một" và "nhiều". Hơn nữa cùng với sự phát triển của xã hội, phương pháp đếm giản đơn cũng không thể không ra đời.

Phát huy tính tích cực, chủ động của sinh viên qua hoạt động tự định hướng học tập.
21:33 24/05/2021
Cùng với xu thế hội nhập, toàn cầu hoá, sự phát triển mạnh mẽ của công nghệ thông tin, sự gia tăng gấp bội của tri thức đòi hỏi giáo dục đào tạo phải đổi mới nội dung dạy học và phương pháp dạy học để đào tạo những con người có đủ năng lực và phẩm chất đáp ứng nhu cầu của thực tiễn. Ưu tiên hàng đầu cho việc nâng cao chất lượng dạy và học, đổi mới phương pháp dạy và học
![Nghiên cứu tính chất cấu trúc của các cluster [〖Mo〗_6 X_14 ]^- (X = F, Cl, Br, I) bằng phương pháp phiếm hàm mật độ](/uploads/no_images.jpg)
Nghiên cứu tính chất cấu trúc của các cluster [〖Mo〗_6 X_14 ]^- (X = F, Cl, Br, I) bằng phương pháp phiếm hàm mật độ
21:47 19/05/2021
Tính chất cấu trúc của cluster Mo6X14 (X = F, Cl, Br, I) ở 23 EM đã được nghiên cứu bằng phương pháp phiếm hàm mật độ ở mức độ lý thuyết PBE/TZ2P. Kết quả nghiên cứu cho thấy dạng đối xứng nhóm điểm bền vững của cluster Mo6F14 và Mo6I14 là D4h, trong khi của cluster Mo6Cl14 và Mo6Br14 lại bền ở dạng đối xứng nhóm điểm C2v. Sự biến dạng của nhân kim loại trong các cluster đã được chứng minh giảm dần khi đi từ Flo đến Iốt. Việc xem xét đến ảnh hưởng tương quan trong sự gần đúng ZORA và tương tác spin – orbit trong tính toán ít ảnh hưởng đến tính chất cấu trúc hình học của các cluster.
PHƯƠNG PHÁP HỌC TIẾNG ANH CHUYÊN NGÀNH HIỆU QUẢ BẠN CẦN BIẾT
10:14 23/12/2020
Tiếng Anh chuyên ngành quan trọng là thế, vậy bạn đã biết cách học sao cho hiệu quả chưa? Nếu chưa tìm ra phương pháp tối ưu nào cho mình, hãy cùng đọc bài viết dưới đây sẽ bật mí cho bạn 5 phương pháp học tiếng Anh chuyên ngành sao cho hiệu quả nhất nhé!
Tìm hiểu về nguồn gốc Hình học
21:41 12/12/2020
Hình học (geometry) bắt nguồn từ tiếng Hy Lạp cổ: geo- "đất", -metron "đo đạc", nghĩa là đo đạc đất đai, là ngành toán học nghiên cứu các liên hệ không gian được con người nghiên cứu từ thời cổ đại. Hình học cổ điển tập trung vào xây dựng các hình dựa trên compa và thước kẻ. Euclid đã cách mạng hóa hình học bằng cách giới thiệu phương pháp chứng minh toán học và các tiên đề mà ngày nay vẫn còn sử dụng. Cuốn sách của ông được coi là sách giáo khoa có ảnh hưởng nhất mọi thời đại, và được phương Tây học tập cho đến ngày nay

NGHIÊN CỨU LÝ THUYẾT HẤP PHỤ CO2 VÀ H2 TRÊN CLUSTER Fe5 BẰNG PHƯƠNG PHÁP PHIẾM HÀM MẬT ĐỘ GGA-PBE
10:17 24/11/2020
Sự hấp phụ CO2 và H2 bởi cluster kim loại Fe5 được nghiên cứu bằng phương pháp phiếm hàm mật độ GGA-DFT với phiếm hàm tương quan trao đổi PBE. Kết quả nghiên cứu cho thấy quá trình hấp phụ CO2 là hấp phụ hóa học (Ehp = -184.416 kJ/mol), trong khi đó sự hấp phụ H2 chủ yếu là hấp phu vật lý (Ehp = -64.800kJ/mol).

Những “bí kíp” giúp sinh viên học online “khỏe ra” trong mùa dịch Covid-19
22:21 29/04/2020
Dù không thể thay thế hoàn toàn phương pháp học tập truyền thống nhưng trước tình hình dịch bệnh Covid-19 tiếp tục diễn biến nguy hiểm, khó lường như hiện nay, dạy và học online được đánh giá là giải pháp tối ưu nhất. Thực tế cũng cho thấy, học online đang ngày càng phổ biến, là phương pháp học hiện đại được nhiều người ưa chuộng. Tuy nhiên, không phải ai cũng biết cách học online tốt nhất để tận dụng ưu thế của internet.

THỐNG KÊ BAYES TRONG MÔ HÌNH CHUẨN, MÔ HÌNH HỒI QUY
15:37 18/09/2019
Làm thế nào chỉ với một bộ mẫu dữ liệu và sử dụng thông tin tiên nghiệm để có thể ước lượng giá trị của tham số tại thời điểm thu thập dữ liệu đó? Thống kê Bayes là một trong những câu trả lời cho câu hỏi này. Khởi điểm của phương pháp này là định lý Bayes quen thuộc. Đây là một lĩnh vực khá thú vị, mới và mang màu sắc hiện đại
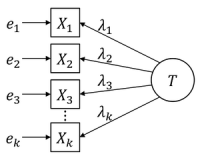
PHƯƠNG PHÁP PHÂN TÍCH ĐỘ TIN CẬY CRONBACH ALPHA VÀ PHÂN TÍCH NHÂN TỐ EFA TRONG CÁC PHÂN TÍCH ĐỊNH LƯỢNG
07:20 29/08/2019
Phân tích EFA là một bước rất quan trọng khi thực hiện phân tích dữ liệu định lượng bằng SPSS trong một bài nghiên cứu khoa học. Khi kiểm định một lý thuyết khoa học, chúng ta cần đánh giá độ tin cậy của thang đo (phân tích Cronbach Alpha) và giá trị của thang đo (EFA).
Sự ổn định mũ của hệ phương trình vi phân phi tuyến theo phương pháp hàm Lyapunov
09:40 22/04/2019
Trong bài báo này, chúng tôi sử dụng phương pháp hàm Lyapunov đưa ra điều kiện đủ để hệ phương trình vi phân phi tuyến ổn định mũ bằng cách xác định tựa hàm Lyapunov. Ngoài ra, trong trường hợp phương trình vi phân phi tuyến có điểm cân bằng ổn định, thì chỉ ra được công thức xác định hàm Lyapunov trong lân cận compact của điểm cân bằng.
- Trường Đại học Sao Đỏ tổ chức “Tết sum vầy – Xuân ơn...
- Trường Đại học Sao Đỏ tổ chức hội nghị Giảng viên chủ...
- Khoa Khoa học cơ bản Hội thảo khoa học bộ môn với chủ...
- Khoa Khoa học cơ bản bồi dưỡng giảng viên với chuyên...
- Khoa Khoa học cơ bản Hội thảo khoa học bộ môn với chủ...
- VIET (Franciscus Viet)
-
Nghị định 73/2015/NĐ-CP
(Quy định về tiêu chuẩn phân tầng; khung xếp hạng và tiêu chuẩn xếp...) -
Quyết định số 07/QĐ-TTg của Thủ tướng...
(Về điều chỉnh mức cho vay đối với học sinh, sinh viên) -
Thông tư số 18/2015/TT-BKHCN
(Quy định thi đua, khen thưởng trong lĩnh vực khoa học và công nghệ) -
Thông tư số 43/2015/TT-BLĐTBXH
(Quy định về đào tạo thường xuyên) -
Nghị định số 137/2015/NĐ-CP
(Quy định chi tiết một số điều và biện pháp thi hành Luật Căn cước công...)









