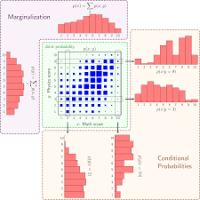
Thống kê Bayes với mô hình chuỗi thời gian
- 28/02/2018 05:06:00 PM
- Đã xem: 2226
Các nhà thống kê Bayes lập luận rằng ngay cả khi người ta có các xác suất chủ quan tiền nghiệm rất khác nhau, bằng chứng mới từ các quan sát lặp đi lặp lại sẽ có xu hướng đưa các xác suất hậu nghiệm của họ lại gần nhau hơn. Trong khi điều này đúng đối với những người duy lý hoàn hảo với các khuynh hướng tương đồng trong việc suy xét mức độ tin tưởng, các khác biệt đủ lớn trong các khuynh hướng này có thể (và thường) gây cản trở lớn lao đối với quá trình hội tụ này.

Cách viết abstract
- 24/01/2018 08:53:00 AM
- Đã xem: 16815
Tựa đề và bản tóm tắt là hai phản chiếu đầu tiên đập vào mắt của người đọc. Đây cũng là phần mà đại đa số người đọc đọc trước khi quyết định có nên đọc tiếp hay không. Tất nhiên, tựa đề và bản tóm tắt là hai phần được đưa vào danh mục của thư viện điện tử. Do đó, nhà nghiên cứu cần phải để tâm suy nghĩ cẩn thận khi soạn hai phần này sao cho thu hút sự chú ý của người đọc. Nhiều người nói rằng abstract là văn bản viết trước, nhưng trong thực tế thì đây là phần sau cùng của một bài báo khoa học.

Giải phương trình tích phân Fedholm loại 2 bằng phương pháp thác triển theo tham số
- 18/01/2018 03:31:00 PM
- Đã xem: 2181
Phương pháp thác triển theo tham số giải phương trình toán tử được nghiên cứu trong các công trình của Trenoghin V.A., Fonarov A.A. và Gaponenco Iu. L. Trong bài viết này tôi nghiên cứu ứng dụng của phương pháp nói trên qua việc giải gần đúng phương trình toán tử, với toán tử tích phân Fredholm.

Ma trận đồng dạng - sự đồng dạng với ma trận tam giác
- 15/01/2018 08:58:00 AM
- Đã xem: 3545
Ma trận không thỏa mãn các điều kiện để chéo hóa thì có thể tam giác hóa ma trận đó cũng là rất hữu ích.

Trường hấp dẫn và sóng hấp dẫn
- 05/01/2018 10:20:00 AM
- Đã xem: 1625
Sóng hấp dẫn sinh ra và truyền đi do sự dao động của trường hấp dẫn, đó là sự gợn sóng trong không - thời gian, được tạo ra bởi sự chuyển động của các vật thể có khối lượng lớn. Sự bóp méo không-thời gian truyền đi với tốc độ ánh sáng. Mọi vật thể nằm trong đường đi của nó sẽ cảm nhận được trọng lực thuỷ triều, tác dụng theo phương vuông góc với hướng truyền của sóng.

Momen động lượng và các ứng dụng trong tự nhiên, khoa học, kỹ thuật
- 27/12/2017 02:48:00 PM
- Đã xem: 7008
Định lý biến thiên và định luật bảo toàn mô men động lượng mang tính chất tổng quát rất lớn và nó chi phối rất nhiều các hiện tượng trong tự nhiên, cũng như ứng dụng trong khoa học kĩ thuật. Bài viết dưới đây tìm hiểu 1 số ứng dụng của mô men động lượng nói chung trên thực tế.

Suy luận Bayes cho biến ngẫu nhiên
- 22/12/2017 08:23:00 AM
- Đã xem: 1759
Ở phần trước ta mới dừng lại ở việc xác định xác tiên nghiệm và hậu nghiện bằng định lý Bayes cho biến ngẫu nhiên. Trong phần này tập trung vào việc suy luận Bayes cho biến ngẫu nhiên.

Một số phương pháp giải phương trình phi tuyến
- 12/12/2017 02:56:00 PM
- Đã xem: 5260
Để tìm nghiệm đúng của phương trình phi tuyến là một vấn đề khá khó khăn khi giải toán. Có nhiều bài ta chỉ tìm được nghiệm gần đúng. Đối với phương trình phi tuyến ta có thể sử dụng một số phương pháp giải như: phương pháp lặp đơn, phương pháp dây cung, phương pháp Newton, Raphson…Ta cũng có thể sử dụng phần mềm Maple để giải.

Phép biến đổi Fourier và ứng dụng
- 12/12/2017 02:47:00 PM
- Đã xem: 5904
Phép biến đổi Fourier là một phép toán quan trọng, là công cụ xử lý hình ảnh được sử dụng để phân hủy một hình ảnh vào sin và cosin thành phần của nó. Đầu ra của biến đổi đại diện cho hình ảnh trong Fourier hoặc miền tần số, trong khi hình ảnh đầu vào là miền không gian tương đương.
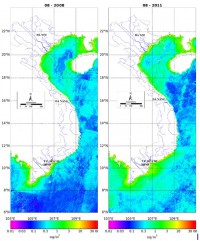
Sử dụng phần mềm R trong phân tích hồi quy tuyến tính
- 21/11/2017 03:47:00 PM
- Đã xem: 2117
Năm 1996, trong một bài báo quan trọng về tính toán thống kê, hai nhà thống kê học Ross Ihaka và Robert Gentleman thuộc trường đại học Auckland, New Zealand phát họa một ngôn ngữ mới cho phân tích thống kê mà họ đặt tên là R.

Đồng vị phóng xạ và một số ứng dụng
- 11/11/2017 12:24:00 AM
- Đã xem: 1654
Đối với cơ thể sống, các tia phóng xạ có khả năng phá hủy cơ thể ở cấp độ tế bào, các dãy AND có thể bị đứt gãy, hư hại hoặc bị sắp xếp lại…đây cũng là nguyên nhân gây ra các bệnh như đột biến, dị tật hoặc ung thư. Tuy nhiên với sự phát triển của khoa học kỹ thuật, con người không những đã kiểm soát được tia phóng xạ mà còn khai thác các đặc tính của chúng để phục vụ chính chúng ta.

Phương pháp bình phương tối thiểu trong dự báo
- 11/11/2017 12:16:00 AM
- Đã xem: 2995
Bài viết trình bày phương pháp bình phương tối thiểu cho một chuỗi thời gian cũng như trong việc kết hợp các mô hình dự báo khác nhau. Tính hiệu quả của phương pháp được minh họa thông qua ví dụ thực tế. Kết quả cho thấy, việc kết hợp nhiều mô hình dự báo bằng phương pháp bình phương tối thiểu cho sai số trung bình bé hơn so với các mô hình dự báo thông thường.
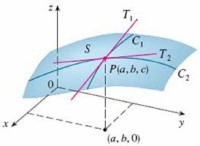
Sử dụng phương pháp số để giải gần đúng phương trình đạo hàm riêng
- 11/11/2017 12:09:00 AM
- Đã xem: 2413
Phương trình đạo hàm riêng thường xuyên xuất hiện trong các bài toán ứng dụng của lý thuyết thuỷ động học, cơ học lượng tử, điện học, điện - từ trường,… Đa số các bài toán này rất phức tạp, nhiều bài toán không có nghiệm theo nghĩa cổ điển. Vấn đề tìm nghiệm đúng của các phương trình đạo hàm riêng không thể và cũng không cần thực hiện trong mọi trường hợp. Bởi vậy, ta dẫn đến việc chỉ tìm được nghiệm gần đúng của các phương trình đạo hàm riêng và cũng từ đó xuất hiện các phương pháp để giải gần đúng các phương trình đó.
Phát triển chương trình đào tạo theo định hướng phát triển
- 10/11/2017 11:58:00 PM
- Đã xem: 13150
Trong báo cáo này, chúng tôi trình bày các cách tiếp cận trong xây dựng chương trình đào tạo, đồng thời làm rõ ưu điểm và nhược điểm của từng cách tiếp cận. Trên cơ sở đó đề xuất một số yêu cầu khi xây dựng chương trình đào tạo theo định hướng phát triển.
- Trường Đại học Sao Đỏ tổ chức “Tết sum vầy – Xuân ơn...
- Trường Đại học Sao Đỏ tổ chức hội nghị Giảng viên chủ...
- Khoa Khoa học cơ bản Hội thảo khoa học bộ môn với chủ...
- Khoa Khoa học cơ bản bồi dưỡng giảng viên với chuyên...
- Khoa Khoa học cơ bản Hội thảo khoa học bộ môn với chủ...
- VIET (Franciscus Viet)
-
Nghị định 73/2015/NĐ-CP
(Quy định về tiêu chuẩn phân tầng; khung xếp hạng và tiêu chuẩn xếp...) -
Quyết định số 07/QĐ-TTg của Thủ tướng...
(Về điều chỉnh mức cho vay đối với học sinh, sinh viên) -
Thông tư số 18/2015/TT-BKHCN
(Quy định thi đua, khen thưởng trong lĩnh vực khoa học và công nghệ) -
Thông tư số 43/2015/TT-BLĐTBXH
(Quy định về đào tạo thường xuyên) -
Nghị định số 137/2015/NĐ-CP
(Quy định chi tiết một số điều và biện pháp thi hành Luật Căn cước công...)









