Nghiên cứu - Trao đổi


Học vụ sinh viên	Học tập trực tuyến	Thư viện điện tử	Ký túc xá

Ứng dụng của một số hợp kim thường gặp

25/10/2018 09:55:00 AM
Đã xem: 1539

Sự phát triển của khoa học công nghệ đòi hỏi phải có thiết bị máy móc hiện đại hỗ trợ, và để thỏa mãn nhu cầu đó phải cần có một hợp kim mới đáp ứng. Ví dụ sự phát triển nhảy vọt của ngành hàng không (1903) gắn với việc ra đời của hợp kim Đu ra, gắn liền với phát triển cơ khí là thép không rỉ (1912), hợp kim Ti (1960), thép kết cầu có đệ bền cao (1965), kim loại nhớ hình (1990)…Ngày nay, khoa học kỹ thuật ngày càng phát triển, các nhà khoa học vẫn tiếp tục nghiên cứu để tạo ra các hợp kim có tính năng ngày càng ưu việt hơn về cả cơ tính lẫn các tính chất vật lý, hóa học đặc biệt

Ứng dụng và thực tế khai thác đất hiếm

05/10/2018 02:36:00 PM
Đã xem: 1378

Đất hiếm đã trở thành loại nguyên liệu tối cần thiết cho các ngành công nghệ mũi nhọn tại các quốc gia phát triển. Đất hiếm có mặt trong hầu hết các sản phẩm công nghệ cao ngày nay từ chiếc máy nghe nhạc bỏ túi iPod cho đến xe hơi, tên lửa, tàu vũ trụ… Nên nguồn tài nguyên này còn được ví như: “Vũ khí của thế kỷ”, “Vitamin của ngành công nghiệp hiện đại”, “muối của cuộc sống” với cuộc cách mạng công nghệ cao.

Phóng xạ và một số ứng dụng trong cuộc sống

21/09/2018 10:15:00 AM
Đã xem: 2860

Các đồng vị phóng xạ với các đặc điểm riêng của chúng đã và đang được khai thác tích cực trong cuộc sống. Khoa học phát triển đã đưa các đồng vị phóng xạ áp dụng vào hầu hết các lĩnh vực như công nghiệp, nông nghiệp, y học, thực phẩm góp phần nâng cao chất lượng đời sống và bảo vệ sức khỏe con người. Tuy nhiên các tác hại mà chất phóng xạ gây ra sẽ vô cùng khủng khiếp nếu như không được quản lý và sử dụng đúng quy định

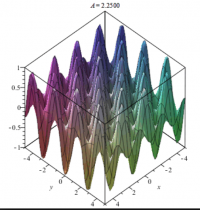
Phép dịch chuyển

17/08/2018 03:32:00 PM
Đã xem: 1224

Trong bài viết này trình bày về sự kết hợp các toán tử giao hoán trong định lý Nhúng với phép dịch chuyển

Một số nghịch lý trong xác suất thống kê

18/05/2018 08:53:00 AM
Đã xem: 2606

Trong xác suất thống kê có những bài toán tưởng chừng như rất đơn giản nhưng dễ tính ra kết quả sai mà khó phát hiện sai ở đâu. Phần này sẽ nêu một số "nghịch lý" trong xác suất để minh họa điều đó. Những nghịch lý này cho thấy chúng ta cần hết sức cẩn thận trong lúc lập mô hình tính toán xác suất, đặc biệt là xác suất có điều kiện, kiểm tra lại những điều tưởng chừng như hiển nhiên, để tránh sai lầm.

Toán tử giải thức bậc phân số

10/05/2018 09:21:00 PM
Đã xem: 1319

Phương trình vi phân hay phương trình sai phân là một phương trình toán học nhằm biểu diễn mối quan hệ giữa một hàm chưa được biết (một hoặc nhiều biến) với đạo hàm của nó (có bậc khác nhau). Phương trình sai phân đóng vai trò cực kì quan trọng trong kĩ thuật, vật lý, kinh tế và một số ngành khác. Do đó xác định nghiệm ổn định của phương trình vi phân có ý nghĩa thực tiễn rất thiết thực.

Học tốt các môn đại cương, tại sao không?

03/05/2018 02:47:00 PM
Đã xem: 4438

Đây là những môn học nặng về lý thuyết và các bạn SV hay cho rằng những môn này: khó học, khó hiểu và rất nhàm chán. Nhiều SV đề xuất bỏ bớt những môn học không cần thiết để tập trung thời gian cho chuyên ngành. Bên cạnh đó, nhiều bạn khác cũng cho rằng cần tạo hứng thú, sinh động, tăng làm việc nhóm, thuyết trình, giảm đọc - chép... ở những môn học đại cương.

Vai trò của môn học vật lý đại cương đối với các học phần thuộc ngành CNKT Điện-Điện tử tại trường đại học Sao Đỏ

27/04/2018 09:31:00 AM
Đã xem: 4134

Trong báo cáo này chúng tôi nghiên cứu vai trò của môn học Vật lý đại cương đối với các môn học thuộc ngành Công nghệ kỹ thuật Điện – Điện tử tại trường Đại học Sao Đỏ. Báo cáo tập trung đánh giá mức độ tác động của những kiến thức, kỹ năng, năng lực mà sinh viên có được sau khi học tập môn học Vật lý đại cương đến sự hình thành những kiến thức, kỹ năng, năng lực trong quá trình học các môn thuộc cơ sở ngành và chuyên ngành. Đồng thời, đánh giá ý nghĩa của môn Vật lý đại cương đối với sự hình thành những năng lực cơ bản của con người trong cuộc sống – Năng lực chung. Kết quả của nghiên cứu cho thấy những kiến thức, kỹ năng, năng lực mà người học đạt được sau khi tham gia môn học Vật lý đại cương có vai trò rất lớn trong việc tạo nền tảng vững chắc để người học lĩnh hội kiến thức từ các học phần thuộc cơ sở ngành, chuyên ngành, cũng như hình thành năng lực chung.

Phân phối chuẩn và một số ứng dụng trong kinh tế

18/04/2018 08:28:00 AM
Đã xem: 5649

Quy luật phân phối chuẩn là quy luật phân phối xác suất được áp dụng rộng rãi trong thực tế. Trong nhiều lĩnh vực của khoa học và đời sống ta đều gặp các biến ngẫu nhiên phân phối chuẩn. Chẳng hạn trong công nghiệp người ta đã xác định được rằng kích thước của các chi tiết do các máy sản xuất ra sẽ phân phối chuẩn nếu quá trình sản xuất diễn ra bình thường.

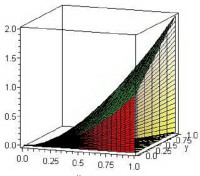
Tích phân bội và ứng dụng

13/04/2018 02:26:00 PM
Đã xem: 2958

Tích phân bội là tích phân của hàm nhiều biến, còn được gọi là tích phân nhiều lớp. Đây là tích phân có nhiều ứng dụng quan trọng trong thực tế. Bài viết này trình bày một vài ứng dụng của tích phân kép trong lĩnh vực hình học như: tính diện tích hình phẳng, thể tích của vật thể, diện tích mặt cong…Một vài ứng dụng trong vật lí, cơ học như: tính khối lượng bản mỏng, mô men quán tính, mô men tĩnh, …

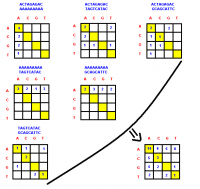
Chéo hóa, tam giác hóa ma trận và ứng dụng

23/03/2018 04:29:00 PM
Đã xem: 5301

Những kiến thức đầu tên về ma trận đã xuất hiện từ những năm 152 TCN, trong cuốn sách “Cửu chương toán thuật” để giải hệ năm phương trình tuyến tính. Thuật ngữ trong tiếng Anh "matrix" (tiếng Latin là "womb", dẫn xuất từ mater—mẹ) do James JosephSylvester nêu ra vào năm 1850.

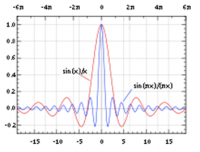
Sự tồn tại của hiện tượng Gibbs trong truyền tín hiệu

14/03/2018 04:18:00 PM
Đã xem: 2408

Hiện tượng Gibbs lần đầu tiên được Henry Wilbraham phân tích trong một bài báo năm 1848. Bài báo thu hút được rất ít sự chú ý cho đến năm 1914, khi nó đã được Heinrich Burkhardt đề cập phân tích trong toán học. Năm 1898, Albert A. Michelson đã phát triển một thiết bị có thể tính toán và tái tổng hợp các chuỗi Fourier.

Điều chế chitosan và ứng dụng trong xử lý nấm mốc.

09/03/2018 03:56:00 PM
Đã xem: 2201

Chitosan từ chitin mang nhiều đặc tính ưu việt như: tính tương thích sinh học, nguồn gốc tái tạo, không độc hại, không gây dị ứng và phân hủy sinh học trong cơ thể, kháng nấm, kháng khuẩn, kháng thể, miễn dịch, chống huyết khối và có thể chế biến với các hình dạng khác nhau tùy vào nhu cầu sử dụng như: sơi, bột, màng, hạt, bọt biển, dung dịch, gel, viên nang…

Phương pháp Euler giải phương trình vi phân

02/03/2018 09:05:00 AM
Đã xem: 10082

Phương pháp Euler là một phương pháp bậc một, có nghĩa là sai số cục bộ (sai số mỗi bước) tỷ lệ thuận với bình phương của kích thước bước, và sai số tổng thể (sai số tại một thời điểm nào đó) tỷ lệ thuận với kích thước bước. Phương pháp Euler thường phục vụ như là cơ sở để xây dựng các phương pháp phức tạp hơn.

Thống kê Bayes với mô hình chuỗi thời gian

28/02/2018 05:06:00 PM
Đã xem: 1957

Các nhà thống kê Bayes lập luận rằng ngay cả khi người ta có các xác suất chủ quan tiền nghiệm rất khác nhau, bằng chứng mới từ các quan sát lặp đi lặp lại sẽ có xu hướng đưa các xác suất hậu nghiệm của họ lại gần nhau hơn. Trong khi điều này đúng đối với những người duy lý hoàn hảo với các khuynh hướng tương đồng trong việc suy xét mức độ tin tưởng, các khác biệt đủ lớn trong các khuynh hướng này có thể (và thường) gây cản trở lớn lao đối với quá trình hội tụ này.