Tìm hiểu về nguồn gốc Hình học
- Thứ bảy - 12/12/2020 21:41
- In ra
- Đóng cửa sổ này
|
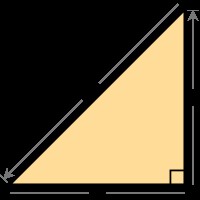
Trước Thales mỗi người đo đạc hoặc nhà hình học đều phải tìm những “kỹ xảo” để đo các khoảng cách, các bề mặt v.v… Nhà triết học và toán học Hy lạp Thales de Milet (thế kỷ VII-VI trước CN) đã có ý tưởng tài tình đo các chiều cao nhờ dùng bóng vào lúc mà “bóng bằng với vật”, nghĩa là vào lúc các tia nắng chiếu xuyên một góc 45 độ. Để đo chiều cao của Đại Kim tự tháp ông đã cải tiến phương pháp của mình bằng cách sử dụng các tia nắng ở bất kỳ lúc nào. Và ông đã có thể dừng lại ở đó, song toàn bộ giá trị công việc của ông là muốn xuất phát từ thực nghiệm để xây dựng nên một lý thuyết: việc sử dụng các tia sáng mặt trời đã cho phép ông nghiên cứu các đường thẳng song song và mối liên hệ giữa độ dài hình chiếu và độ dài ban đầu. Rồi ông đã phát biểu một định lý mà từ đó được gọi theo tên ông là Định lý Thales: “Các đường thẳng song song chiếu những đoạn dài tỷ lệ từ đường thẳng này lên đường thẳng khác”. Như vậy là ông đã rút ra hình học từ cuốn sổ ghi chép các kỹ thuật bằng cách đưa vào đó quan điểm suy diễn và chứng minh của toán học.  Xuất phát từ các công trình của Thales về các đường thẳng song song và cũng với tinh thần chứng minh, Pythagore, nhà triết học và toán học Hy lạp ở thế kỷ VI trước CN đã quan tâm đến hình chiếu vuông góc và đã chứng minh được định lý mang tên ông. Định lý đó thiết lập được mối liên hệ giữa chiều dài các cạnh của một tam giác vuông. Mối quan hệ đó đã được biết đến từ thời loài người cần đo đạc, song chính Pythagore là người đầu tiên đã chứng minh được nó.
 Nhà toán học Hy lạp là Euclide (thế kỷ III trước CN) chủ yếu đã tổng hợp các công trình của người đi trước trong tác phẩm “Nguyên lý” ông đã hệ thống các kiến thức của thời đại mình, đồng thời chứng minh lại toàn bộ xuất phát từ năm tiên đề được coi như đúng dù rằng không được chứng minh. Tiên đề cơ bản và quen thuộc nhất là: “Qua một điểm bên ngoài một đường thẳng, chỉ có thể kẻ một đường thẳng song song với đường thẳng đó”. Cho đến thế kỷ XIX, các nhà toán học vẫn nghĩ rằng có thể chứng minh được tiên đề đó. Bởi vậy ở thế kỷ thứ XVIII nhiều nhà toán học đã uổng công thử chứng minh nó bằng phản chứng.
Việc sử dụng các số để xác định một cách tính vị trí của một điểm trên một bề mặt đã được biết đến từ thời Archimede (thế kỷ III trước CN). Nhưng mãi tới thế kỷ XVII thì tọa độ mới được sử dụng một cách có hệ thống đối với các bài toán hình học. Có truyền thuyết rằng nhà triết học và toán học người Pháp R. Descartes (1596-1650) đã nảy ra ý tưởng về tọa độ khi ông nhìn thấy một con côn trùng bay trước những ô kính cửa sổ của mình. Khám phá đó đã cho phép khảo sát các bài toán hình học theo phương pháp đại số; rồi nhờ có nhà toán học Pháp P. de Fermat (1601-1665) đã bắt đầu xuất hiện hình học giải tích trong đó các phương trình và đường cong có liên quan với nhau. |