Các giai thoại về nhà toán học Gauss
- Thứ ba - 16/08/2022 22:48
- In ra
- Đóng cửa sổ này
Chắc hẳn thời đi học, đã từng có ít nhất một lần chúng ta được nghe cái tên Gauss, nhà toán học người Đức. Thật vậy, người ta đánh giá rằng nếu trừ cái tên Newton ra thì hiếm có một nhà toán học nào để lại nhiều ảnh hưởng cho nền toán học hiện đại như Carl Gauss. Ngoài các các định lý, phát minh … thần đồng này còn để lại cho chúng ta nhiều giai thoại thú vị. Bài viết này tổng hợp một số giai thoại nổi tiếng về nhà Toán học Gauss.
1. Giai thoại: “Học tính trước khi học nói”
 Johann Carl Friedrich Gauss (30/4/1777 - 23/2/1855).
Viết chính xác tên của ông là Johann Carl Friedrich Gauss, ông sinh ngày 30 tháng 4 năm 1777 và mất ngày 23 tháng 2 năm 1855. Gauss được người đời ca tụng là “Hoàng tử của các nhà toán học”, thế nhưng danh hiệu này không hoàn toàn xuất phát từ những đóng góp của ông cho nền toán học mà còn bởi vì từ nhỏ, ông vốn là một thần đồng có khả năng tính toán hơn người. Gia đình của Gauss thuộc tầng lớp lao động nghèo trong xã hội Đức, mẹ của ông thậm chí còn không biết chữ và có rất ít kiến thức. Vì không biết chữ, bà không thể ghi lại ngày sinh của Gauss mà chỉ nhớ rằng ông được sinh ra vào tháng 4, trước lễ Thăng Thiên 8 ngày và sau lễ Phục Sinh 39 ngày. Khi còn nhỏ, nhờ vào những dữ liệu mà mẹ cho mình biết, Gauss đã có thể tính được ngày sinh của mình và phát hiện ra nhiều phương pháp tính ngày theo lịch.Nhiều giai thoại kể rằng Gauss đã tính toán cực kì nhạy bén từ năm lên 3, cái tuổi mà đám con nít vẫn khóc nhè giành nhau cây kẹo mút. Một hôm ông vô tình gặp ba của mình đang tính toán các ghi chép bán hàng, ông chợt nhận thấy một sai sót nhỏ và báo cho ba biết. Người ba lúc bấy giờ nửa tin nửa ngờ vì con trai của mình chỉ mới 3 tuổi thì làm sao có thể biết đúng hay sai, mặc dù vậy ông vẫn cẩn thận kiểm tra và tính lại. Thật bất ngờ khi đúng là ông đã tính sai ở ngay chỗ mà Gauss mách mình. 2. Giai thoại: “Tính nhanh tổng các số tự nhiên từ 1 đến 100” Năm Gauss lên 7, lại tiếp tục xuất hiện một giai thoại khác về khả năng tính toán của ông. Gauss đi học ở lớp và thầy giáo đưa ra một đề toán hãy tính tổng của các số từ 1 đến 100. Đây là một bài toán dạng cấp số cộng đơn giản với chúng ta ngày nay, nhưng với một đứa trẻ lên 7 thì đây là một câu hỏi tương đối phức tạp. Suy nghĩ trong vài giây, Gauss tuyên bố đã giải được thế nhưng thầy giáo cho rằng ông không thể giải quyết nhanh đến thế nên bảo Gauss hãy xem kỹ lại, có thể tính bị sai đấy. Nhưng Gauss không hề sai, ông giải thích một cách nhanh gọn: "Ta lấy số đầu tiên cộng với số cuối cùng rồi số thứ 2 cộng với số trước số cuối cùng và cứ thế ta sẽ có những cặp số mà tổng số mỗi cặp là 101.Cứ xếp từng cặp như thế (từ 1 đến 100)  ta sẽ có 50 cặp. Vậy thì tổng số các số nguyên từ 1 đến 100 sẽ bằng: 50 cặp * 101 = 5050. ta sẽ có 50 cặp. Vậy thì tổng số các số nguyên từ 1 đến 100 sẽ bằng: 50 cặp * 101 = 5050.
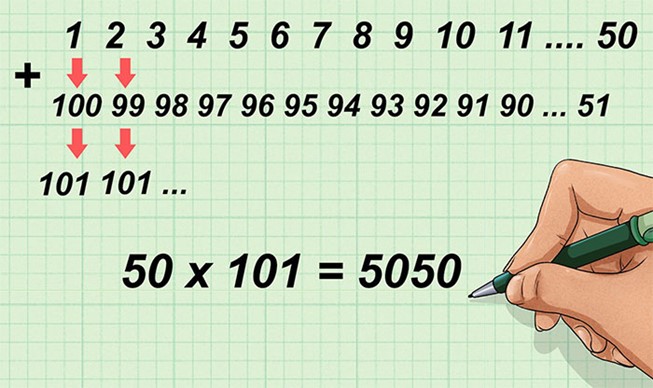 Thực vậy: 1+100=101 2+99=101 3+98=101 ........ 50+51=101 50 cặp * 101=5050. 3. Giai thoại: “Cậu học trò 19 tuổi giải thành công bài toán cổ 2000 năm” Khoảng 300 năm trước Công Nguyên, các nhà toán học từ thời Euklid luôn cố gắng giải quyết một vấn đề nghe thì tưởng chừng đơn giản nhưng chưa hề có ai làm được một cách triệt để. Đó là tìm cách dựng các đa giác đều chỉ bằng thước kẻ và compa. Lúc bấy giờ, người ta chỉ tìm được cách dựng ra hình vuông, tam giác đều, ngũ giác đều và gần thời của Gauss nhất thì cũng chỉ dựng được 15 cạnh đều mà thôi. Quay trở lại về Gauss, lúc này là một chàng trai chưa đầy 19 tuổi đang học Đại học. Mỗi ngày, thầy hướng dẫn của ông sẽ giao riêng cho ông 2 đề toán để làm mỗi ngày, coi như bài tập về nhà. Như thường lệ, hai bài toán mà thầy đưa ra thường không đủ sức cầm chân Gauss và ông chỉ tốn vài tiếng ngắn ngủi là giải quyết được. Song khác với mọi khi, ngày nọ Gauss vô tình tìm thấy thêm một đề toán khác được kẹp vào tập đề của ông. Ông hơi ngạc nhiên vì hôm nay thầy giao cho mình đến 3 bài, thế nhưng ông vẫn bắt tay vào giải nó mà không phàn nàn gì. Đề bài như sau: “Dùng một compa và thước kẻ không khắc độ, vẽ ra một hình có đúng 17 cạnh đều nhau” Rõ ràng đây chính là một trường hợp của bài toán vốn đã tồn tại hơn 2000 năm nay mà chưa ai có thể giải được một cách tổng quát, hay ít nhất là với trường hợp 17 cạnh. Đề bài này quá khó, không như hai bài trước. Gauss tốn rất nhiều thời gian, từng tiếng trôi qua trong đêm và ông phải vắt hết tất cả kiến thức và trí óc của mình để tìm cách dựng hình. Gauss miệt mài với bút, giấy, compa và thước tới tận sáng. Lúc này Gauss đã hoàn thành được bài toán. 
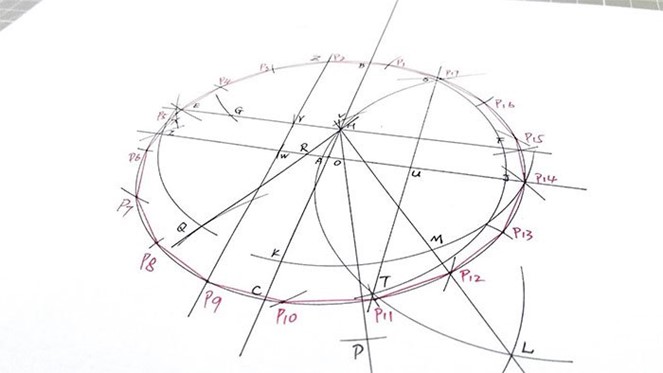 Mặc dù đã giải được, nhưng Gauss vẫn cảm thấy hổ thẹn vì cho rằng mình đã giải bài này quá lâu. Ông gặp thầy hướng dẫn và nói rằng “Em xin lỗi vì đã phụ lòng công sức của thầy, bài toán thứ 3 em đã phải mất cả đêm mới làm được…”. Người thầy bất ngờ vì câu nói, vội cầm lấy tập của Gauss xem xét và đứng trơ người vì quá hoảng hồn. Người thầy hỏi lại: Chính em làm bài này thật à? Dạ, tất nhiên rồi, nhưng em phải tốn cả đêm để hoàn tất bài này. Em thật kém cỏi - Gauss đáp lại. Người thầy kêu học trò của mình ngồi xuống, yêu cầu Gauss tự tay vẽ lại trước mặt mình một hình đa giác 17 cạnh đều. Gauss vẽ lại trong sự trầm trồ của người thầy, sau khi hoàn tất, người thầy nói rằng: “Em có biết đây là bài toán trước giờ chưa ai có thể giải được, kể cả Archimedes hay Isaac Newton không? Bài toán này đã có niên đại hơn 2000 năm, và em chỉ giải nó trong một đêm, em thật sự là một thiên tài!”. Nhiều người cho rằng đề toán này là do chính người thầy đưa cho Gauss một cách có chủ ý để thử thách cậu học trò, nhưng có người cũng cho rằng bản thân người thầy cũng đang bí trong việc giải quyết vấn đề khó và vô tình để lọt đề bài vào tập đề của Gauss. Nhưng dù thế nào thì khoảnh khắc ấy cũng đã đánh dấu một cột mốc lớn của huyền thoại toán học. Gauss bất ngờ vì những gì người thầy nói với mình, từ thất vọng, ông chuyển thành sung sướng và hạnh phúc. Hình đa giác đều 17 cạnh và bài toán dựng hình của nó trở thành một trong những công trình mà Gauss tâm đắc nhất cuộc đời mình. Thậm chí ông yêu cầu khi chết, hãy khắc hình này lên bia một của ông. Nhưng thú vị thay, để dựng được hình này trên bia đá là quá khó, do đó người làm bia đã từ chối nguyện vọng của Gauss và ý nguyện của ông không thể hiện thực được. 
 Bia mộ của Gauss hiện tại
Về sau, Gauss chia sẻ và nói lại rằng “Nếu có ai đó nói với tôi rằng đó là một bài toán khó, đã có 2000 năm lịch sử và chưa có ai giải được, thì có lẽ tôi đã bỏ cuộc và không thể hoàn thành đó”. Câu nói này cũng là bài học cho việc, có lẽ nếu chúng ta không biết vấn đề mà chúng ta đang đối mặt khó khăn như thế nào, có lẽ là chúng ta sẽ thực hiện nó tốt hơn là vạch ra rất nhiều thử thách rồi buông xuôi.4. Giai thoại về tính cầu toàn, hoàn hảo của Gauss “Pauca sed matura” Gauss cũng là một người rất cá tính và thích tự mình quyết định hướng đi của mình. Mặc dù nghiên cứu rất nhiều, nhưng ông hiếm khi xuất bản các công trình của mình cho thế giới. Không phải vì ông muốn giữ các kiến thức này của riêng mình mà vì cơ bản là ông cho rằng các nghiên cứu này vẫn chưa được hoàn thiện, hoàn hảo. Động thái này khá giống với việc ông cảm thấy áy náy khi phải mất cả đêm mới hoàn thành xong bài tập của thầy mà mình đã đề cập ở trên. Ông luôn đi theo chủ nghĩa pauca sed matura, có nghĩa là ít nhưng chắc. Vì ít khi xuất bản các công trình nghiên cứu, nên rất nhiều trường hợp người ta phát hiện ra các công trình mà những nhà toán học khác công bố độc lập đã từng xuất hiện trong ghi chép của Gauss trước đó hàng chục năm. Điển hình như việc người ta phát hiện Gauss đã từng khám phá ra hình học phi Euklid, nhưng ông không công bố nên sau đó, công trình này đã được ghi danh bởi Janos Bolyai. Cũng có một giai thoại vui giữa Gauss và Bolyai. Đó là ba của Bolyai, ông Farkas Bolyai từng là một người bạn của Gauss và đã từng tìm cách khám phá ra hình học Euklid dựa và các tiên đề nhưng không thành công. Đến khi Janos Bolyai công bố việc khám phá hình học phi Euklid, Gauss đã viết thư cho Farkas và nói rằng “Để khen công trình này thì khác nào tôi tự khen tôi, vì nó trùng khớp với những gì tôi đã nghĩ và nghiên cứu trong suốt hơn 30 năm qua”. Chính câu nói này đã tạo nên sự căng thẳng trong mối quan hệ của Gauss và cha con nhà Bolyai. Tổng kết: Vì những đóng góp của mình Gauss được vinh danh trên toàn thế giới, và đặc biệt là ở quê hương nước Đức của ông. Từ năm 1989 đến 2001, Đức đã in hình ông và phân bố Gauss do ông tìm ra trên tờ tiền 10 mark. Đồng thời nước này cũng in các con tem kỉ niệm tròn 100 và 200 năm ngày sinh của ông.  Từ năm 1989 đến 2001, Đức đã in hình ông và phân bố Gauss trên tờ tiền 10 mark.
Nhờ các đóng góp về thiên văn học, tên của ông cũng được đặt cho một miệng hố trên Mặt trăng và tiểu hành tinh 1001 Gaussia.Giải thưởng Gauss được thành lập năm 2006, dành tặng cho những thành tựu toán học có ứng dụng vào các ngành khác và cuộc sống. |